0. 知识点

  • 滑动窗口
  • 前缀和数组

滑动窗口算法（快慢指针）

  • 滑动窗口算法技巧主要用来解决子数组、子串问题，比如让你寻找符合某个条件的最长/最短子数组。
  • 它是一个左闭右开的区间
  • 时间复杂度O(N)
    思路：先移动右指针找到可行解，然后移动左指针找到最优解。然后再移动有指针。。。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
// 滑动窗口算法伪码框架
void slidingWindow(string s) {
    // 用合适的数据结构记录窗口中的数据，根据具体场景变通
    // 比如说，我想记录窗口中元素出现的次数，就用 map
    // 如果我想记录窗口中的元素和，就可以只用一个 int
    auto window = ...

    int left = 0, right = 0;
    while (right < s.size()) {
        // c 是将移入窗口的字符
        char c = s[right];
        window.add(c);
        // 增大窗口
        right++;

        // 进行窗口内数据的一系列更新
        ...

        // *** debug 输出的位置 ***
        printf("window: [%d, %d)\n", left, right);
        // 注意在最终的解法代码中不要 print
        // 因为 IO 操作很耗时，可能导致超时

        // 判断左侧窗口是否要收缩
        while (window needs shrink) {
            // d 是将移出窗口的字符
            char d = s[left];
            window.remove(d);
            // 缩小窗口
            left++;

            // 进行窗口内数据的一系列更新
            ...
        }
    }
}

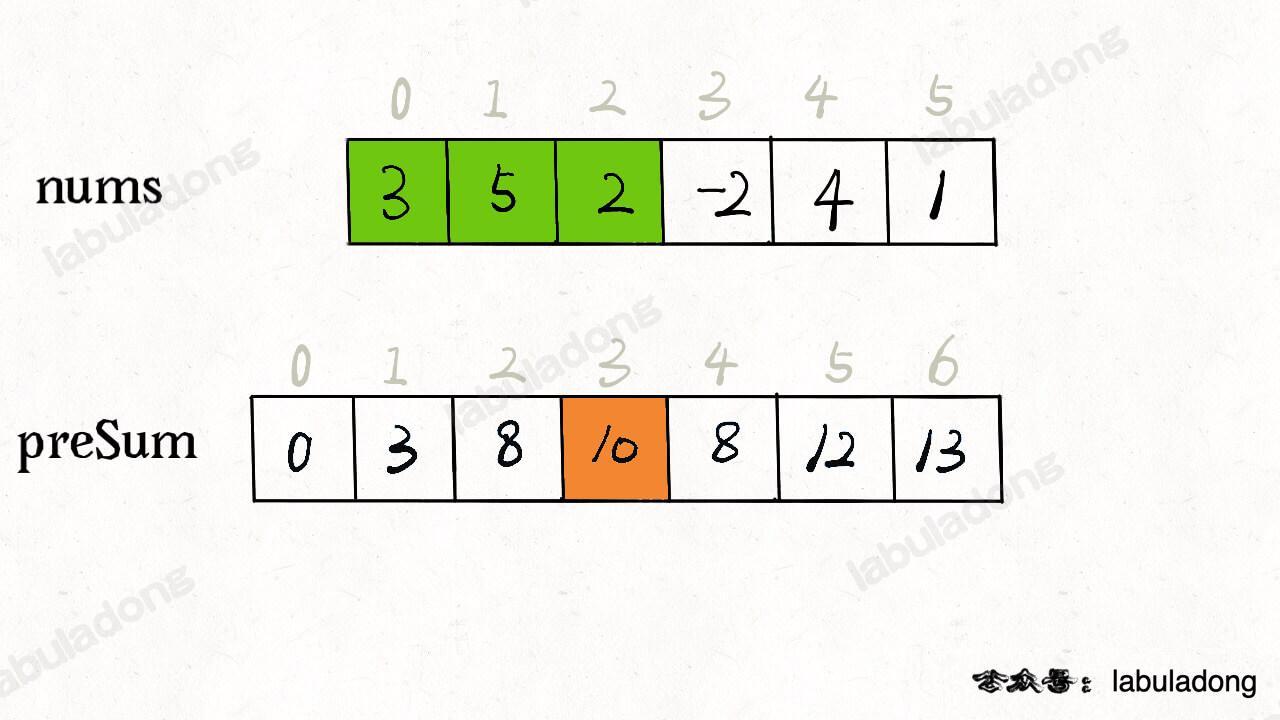
前缀和数组、矩阵

数组

lanuladong
前缀和数组创建
求索引区间 [1, 4] 内的所有元素之和，就可以通过 preSum[5] - preSum[1] 得出。

矩阵


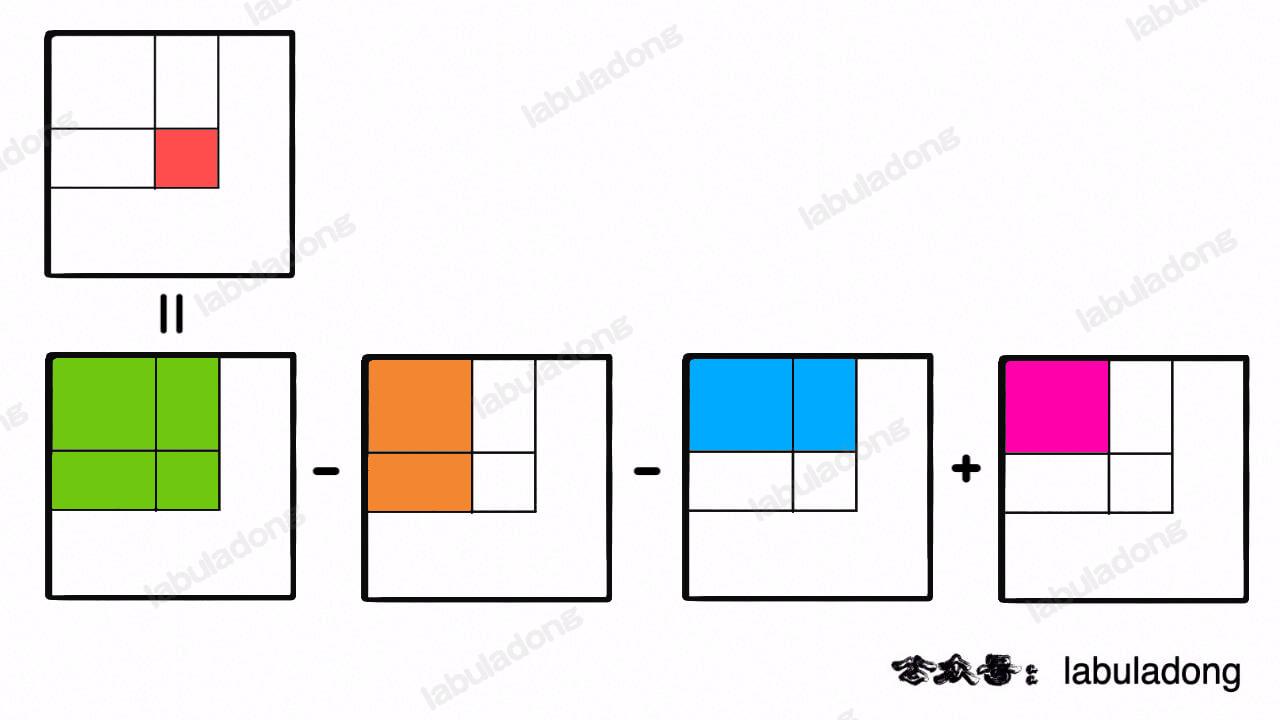
维护和数组类似，对于m*n的矩阵，我们维护一个m+1*n+1的前缀和矩阵。preSum[i][j] = preSum[i-1][j] + preSum[i][j-1] + matrix[i - 1][j - 1] - preSum[i-1][j-1]。

总结：

学习时长：四个半小时。映像比较深刻的就是左闭右开很多时候会减少计算量。

1、209长度最小的子数组

labuladong文章链接
代码随想录文章链接
视频链接
知识点：滑动窗口

给定一个含有 n 个正整数的数组和一个正整数 target 。找出该数组中满足其总和大于等于 target 的长度最小的子数组[numsl, numsl+1, …, numsr-1, numsr] ，并返回其长度。如果不存在符合条件的子数组，返回 0 。

思路： 拿到这道题首先看到是找最小串问题，优先考虑滑动窗口法。滑动窗口法的思路是先移动右指针找到可行解，然后移动左指针找到最优解。这里可行解是满足其总和大于等于 target，最优解是可行解中的最小的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
int minSubArrayLen(int target, vector<int>& nums) {
    int left = 0, right = 0; //初始时区间内没有数据，所以是左闭右开的区间
    int sum = 0;
    int minlen = std::numeric_limits<int>().max();

    //右指针
    while(right < nums.size()){
        sum+=nums[right]; // 移入窗口
        right++;

        // 1、移动右指针找到可行解，可行解的条件就是sum >= target
        // 然后开始移动左指针
        while(sum >= target){
            // 2、移动左指针找到最优解，移出窗口
            int len = right-left;
            if(len<minlen){
                minlen = len;
            }
            sum-=nums[left]; 

            left++;
        }
    }
    if(minlen==std::numeric_limits<int>().max())return 0;
    return minlen;
}

2、59螺旋矩阵II

labuladong文章链接
代码随想录文章链接
视频链接
知识点：滑动窗口

给你一个正整数 n ，生成一个包含 1 到 n2 所有元素，且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。

我的思路：拿到这一题我首先想到的就是按照题目所说的一圈一圈的填充矩阵。除此之外我再也想不到了。。。好好复盘了一下之前做的那些题，没做出来的原因并不是这些框架不会，而是没想出来怎么把这些题抽象成框架出来。。图穷匕见了，还是刷的少了。看了代码随想录之后我发现思路和我是一样的，但是在处理转圈问题上我做题时不够清晰，而且缺乏技巧，他是叠加一个一个的转圈，xy滚动叠加，而我每次重新计算,思路上比我得容易理解很多。还是刷的少了。
按照以上思路的暴力算法：击败6.74%的人，可怜。。。。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
vector<vector<int>> generateMatrix(int n) {
    vector<vector<int>> mat(n,vector<int>(n));
    int data = 1;
    for(int i = 0;i<n/2;i++){
        for(int j = i;j<=n-2-i;j++){
            mat[i][j]=data++;
        }
        for(int j = i;j<=n-2-i;j++){
            mat[j][n-1-i]=data++;
        }
        for(int j = n-1-i;j>=i+1;j--){
            mat[n-1-i][j]=data++;
        }
        for(int j = n-1-i;j>=i+1;j--){
            mat[j][i]=data++;
        }
    }
    if(n%2!=0){
        mat[n/2][n/2]=data;
    }
    return mat;
}

重新优化后好了很多，，但是我发现一般对于边界取不到优先使用左闭右开的区间会省去很多计算量：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
vector<vector<int>> generateMatrix(int n) {
    vector<vector<int>> mat(n,vector<int>(n));
    int data = 1;
    for(int i = 0;i<n/2;i++){
        int k = n-1-i;
        for(int j = i;j<=k-1;j++){
            mat[i][j]=data++;
        }
        for(int j = i;j<=k-1;j++){
            mat[j][k]=data++;
        }
        for(int j = k;j>=i+1;j--){
            mat[k][j]=data++;
        }
        for(int j = k;j>=i+1;j--){
            mat[j][i]=data++;
        }
    }
    if(n%2!=0){
        mat[n/2][n/2]=data;
    }
    return mat;
}

看了代码随想录的视频左闭右开：重新做了大幅提升速度

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
vector<vector<int>> generateMatrix(int n) {
    vector<vector<int>> mat(n,vector<int>(n));
    int data = 1;
    for(int start = 0;start<n/2;start++){
        int x = start;
        int y = start;

        for(;y<n-start-1;y++){
            mat[x][y]=data++;
        }
        for(;x<n-start-1;x++){
            mat[x][y]=data++;
        }
        for(;y>start;y--){
            mat[x][y]=data++;
        }
        for(;x>start;x--){
            mat[x][y]=data++;
        }
    }
    if(n%2!=0){
        mat[n/2][n/2]=data;
    }
    return mat;
}