1、24两两交换链表中的节点

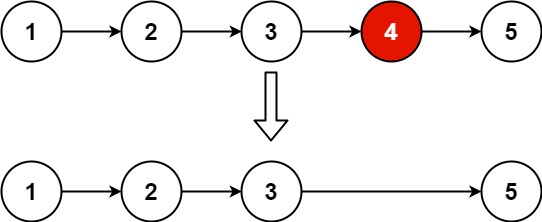
给你一个链表，两两交换其中相邻的节点，并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题（即，只能进行节点交换）。

代码随想录

思路：拿到这道题看到时看到两两交换节点，就想到能不能用双指针，但是对于什么时候用双指针还是有点迷糊的。然后思考能不能用虚拟头节点，思考了以下我只是两两交换节点似乎不和虚拟头节点沾边，我没法用上。写着写着发现我把这两个节点交换时，好像涉及到要把之前的节点连上，把之后的节点连上，之后的节点可以使用cur指针找到，但是之前的节点没法啊。。。于是恍然大悟。.

虚拟头节点、双指针总结： 在处理需要断键重连的链表问题时，如果一下子想不出来，优先思考可不可以用双指针，双指针第一个指针存储last节点，另一个则是cur节点，可以省去很多临时节点。如果第一个元素也需要处理，那就需要前面加上虚拟头节点，方便第一个元素也可以有last。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
ListNode* swapPairs(ListNode* head) {
    if(head == nullptr || head->next == nullptr){
        return head;
    }

    ListNode dumy(0,head);

    ListNode* pre = &dumy, *cur = head;
    while(cur!=nullptr && cur->next != nullptr){
        auto tmp = cur->next->next;

        pre->next = cur->next;
        cur->next->next = cur;
        cur->next = tmp; 

        pre = cur;
        cur = tmp;
    }
    return dumy.next;
}

看了代码随想录之后看到他是直接用了一个指针，从虚拟头节点就开始，这样之后的节点就可以直接next.next…下去。我用双指针的话有last访问之前的节点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    ListNode* swapPairs(ListNode* head) {
        ListNode* dummyHead = new ListNode(0); // 设置一个虚拟头结点
        dummyHead->next = head; // 将虚拟头结点指向head，这样方便后面做删除操作
        ListNode* cur = dummyHead;
        while(cur->next != nullptr && cur->next->next != nullptr) {
            ListNode* tmp = cur->next; // 记录临时节点
            ListNode* tmp1 = cur->next->next->next; // 记录临时节点

            cur->next = cur->next->next;    // 步骤一
            cur->next->next = tmp;          // 步骤二
            cur->next->next->next = tmp1;   // 步骤三

            cur = cur->next->next; // cur移动两位，准备下一轮交换
        }
        ListNode* result = dummyHead->next;
        delete dummyHead;
        return result;
    }
};

2、19删除链表的倒数第N个节点

给你一个链表，删除链表的倒数第 n 个结点，并且返回链表的头结点。

代码随想录

思路： 这题之前看labuladong的博客时刷过，有两种方法：第一种时很直接的，先遍历一遍算出链表总长度l，然后l-n就是需要移除的下标，我们需要找到下标l-n-1的元素就可以移除l-n。第二种是用快慢双指针，快指针先走n步，然后慢指针才开始走，快指针走到头了慢指针对应的元素就是要移除的元素。这两种算法其实复杂度一样，但是双指针的显得更nb。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
ListNode* removeNthFromEnd(ListNode* head, int n) {
  if(head == nullptr) return head;
  ListNode dumy(0,head);
  ListNode *p = &dumy;
  int i = 0;
  while(p!=nullptr){
      p = p->next;
      i++;
  }
  p =  &dumy;
  int idx = i-n-1;
  while(idx--){
      p = p->next;
  }
  p->next = p->next->next;
  return dumy.next;
}

快慢双指针做法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
ListNode* removeNthFromEnd(ListNode* head, int n) {
    if(head == nullptr) return head;
    ListNode dumy(0,head);
    ListNode *fast = &dumy, *low = &dumy;
    int i = n+1;
    while(i--){
        fast = fast->next;
    }
    while(fast!=nullptr){
        low = low->next;
        fast = fast->next;
    }
    low->next = low->next->next;
    return dumy.next;
}

3、面试题02.07链表相交

给你两个单链表的头节点 headA 和 headB ，请你找出并返回两个单链表相交的起始节点。如果两个链表没有交点，返回 null 。题目数据 保证 整个链式结构中不存在环。

代码随想录

思路： 这道题刷过，思路有两个。一是先遍历求各自的长度，然后长的先移动对其短的。另一种是同时遍历A、B链表，哪个遍历完就遍历下一个，这样就能保证两个遍历的一样多，直到遇上相同节点就结束。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
    if(headA==nullptr || headB == nullptr)return nullptr;
    ListNode *p1 = headA,*p2 = headB;
    while(p1!=p2){
        p1 = p1->next;
        p2 = p2->next;
        if(p1 == nullptr && p2 == nullptr)return nullptr;
        else if(p1 == nullptr){
            p1 = headB;
        }
        else if(p2 == nullptr){
            p2 = headA;
        }
    }
    return p1;
}

4、142环形链表II

给定一个链表的头节点 head ，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。
如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。 为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。注意：pos 不作为参数进行传递，仅仅是为了标识链表的实际情况。

代码随想录

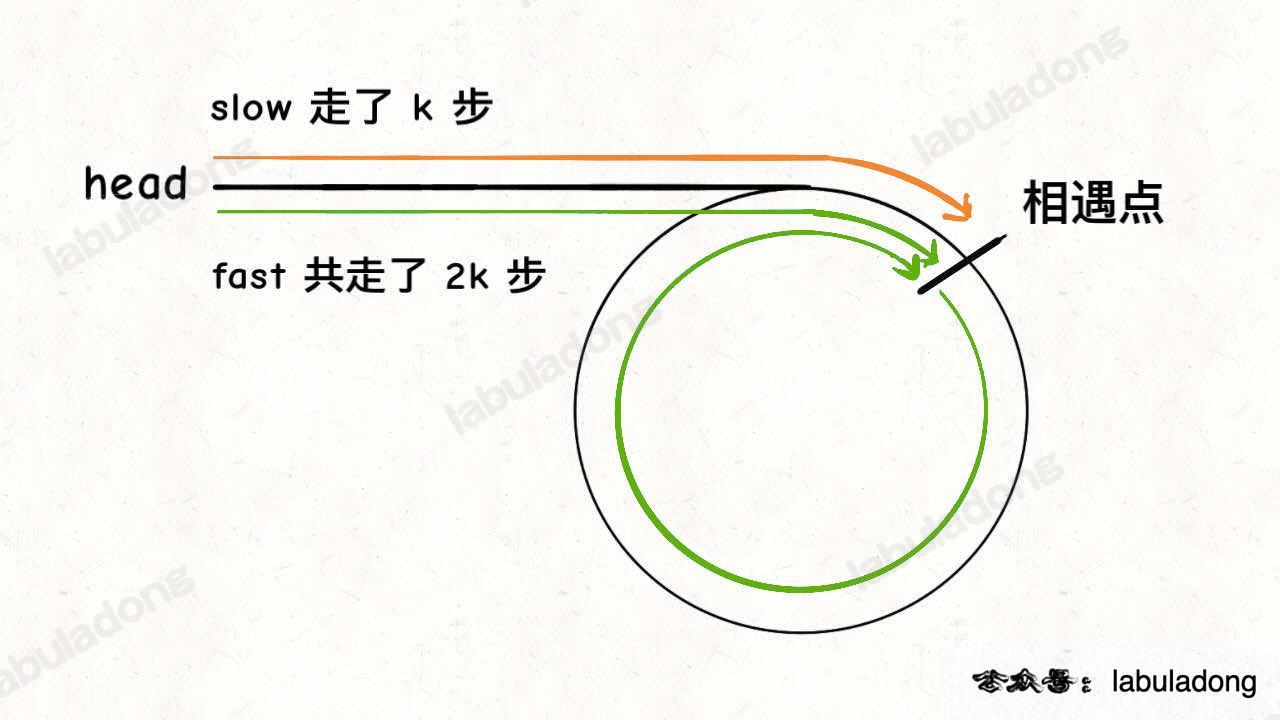
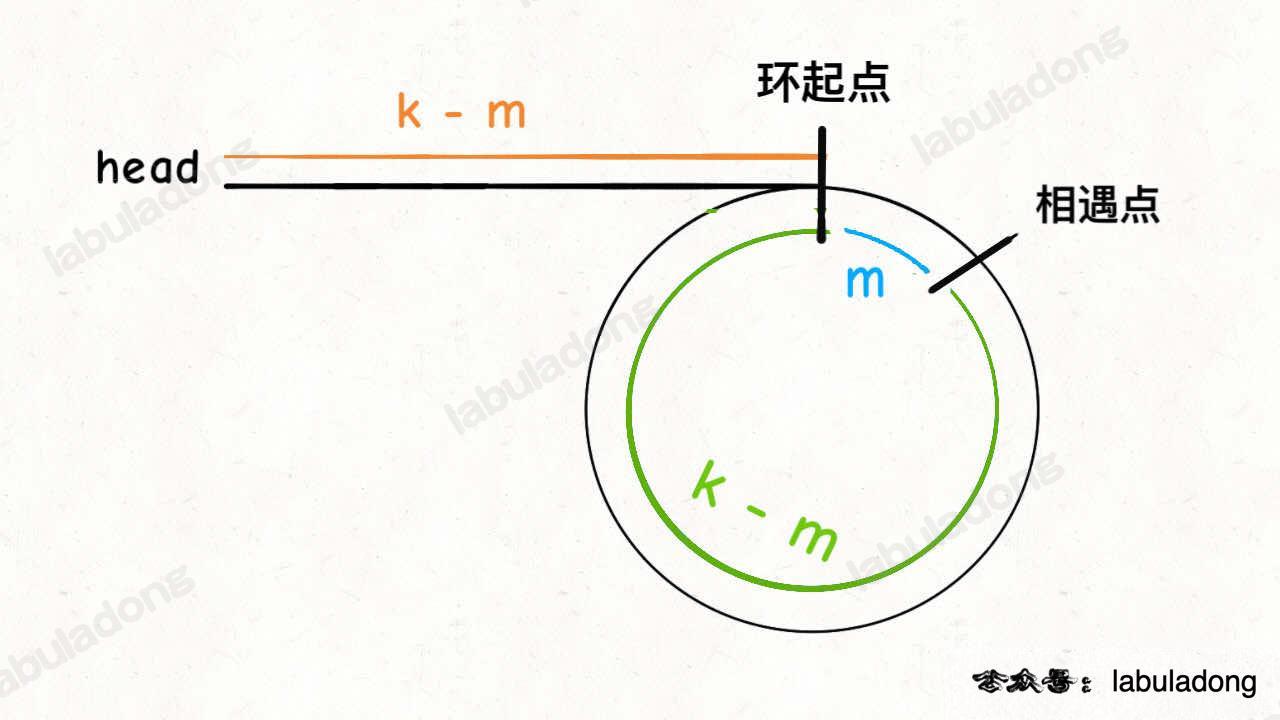
思路： 这道题是判断链表是否有环，有则返回环点。之前刷过，思路上快慢双指针，快指针以两倍速走，慢指针一倍速走，如果有环则快指针早晚追上慢指针，如果没环最后会遇到nullptr。有一个注意的是：快慢指针相遇的位置并不一定是环点。我的思路是先找到相遇点，然后展开成两个链表相遇的问题。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
class Solution {
public:
    ListNode *detectCycle1(ListNode *head) {
        ListNode dumy(0,head);
        ListNode *low = &dumy,*fast = head;
        while(fast != nullptr){
            if(low == fast){
                return low;
            }

            low = low->next;
            if(fast->next == nullptr){
                return nullptr;
            }
            fast = fast->next->next;
        }
        return nullptr;
    }

    ListNode *getIntersectionNode(ListNode *headA, ListNode *headB, ListNode *inse) {
        if(headA==nullptr || headB == nullptr)return nullptr;
        ListNode *end = inse->next;
        ListNode *p1 = headA,*p2 = headB;
        while(p1!=p2){
            p1 = p1->next;
            p2 = p2->next;
            if(p1 == end && p2 == end){
                return p1;
            }
            else if(p1 == end){
                p1 = headB;
            }
            else if(p2 == end){
                p2 = headA;
            }
        }
        return p1;
    }

    ListNode *detectCycle(ListNode *head) {
        auto inse = detectCycle1(head);
        if(inse == nullptr) return inse;
        return getIntersectionNode(head,inse->next,inse);
    }
};

看了labuladong视频和文章之后我悟了。他的做法也是先找环内点，然后双指针一个从头，一个从环内点开始，遇到的就是环起点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        ListNode* fast = head;
        ListNode* slow = head;
        while(fast != NULL && fast->next != NULL) {
            slow = slow->next;
            fast = fast->next->next;
            // 快慢指针相遇，此时从head 和 相遇点，同时查找直至相遇
            if (slow == fast) {
                ListNode* index1 = fast;
                ListNode* index2 = head;
                while (index1 != index2) {
                    index1 = index1->next;
                    index2 = index2->next;
                }
                return index2; // 返回环的入口
            }
        }
        return NULL;
    }
};