代码随想录算法训练第六天|哈希表理论基础|242有效的字母异位词|349两个数组的交集|202快乐数|1两数之和

哈希表理论基础

什么时候用哈希法？

当我们遇到了要快速判断一个元素是否出现集合里的时候，就要考虑哈希法。

Hash表

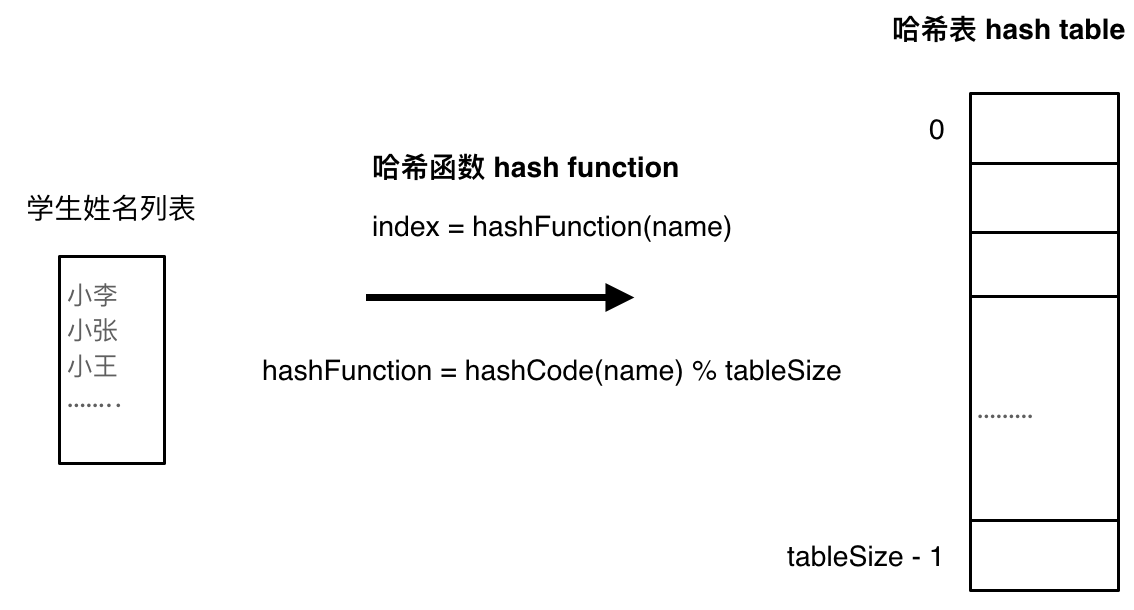
数组就是一张哈希表。我们通过Hash函数把键映射成一个整数值，然后通过取模操作映射到哈希表的索引上。

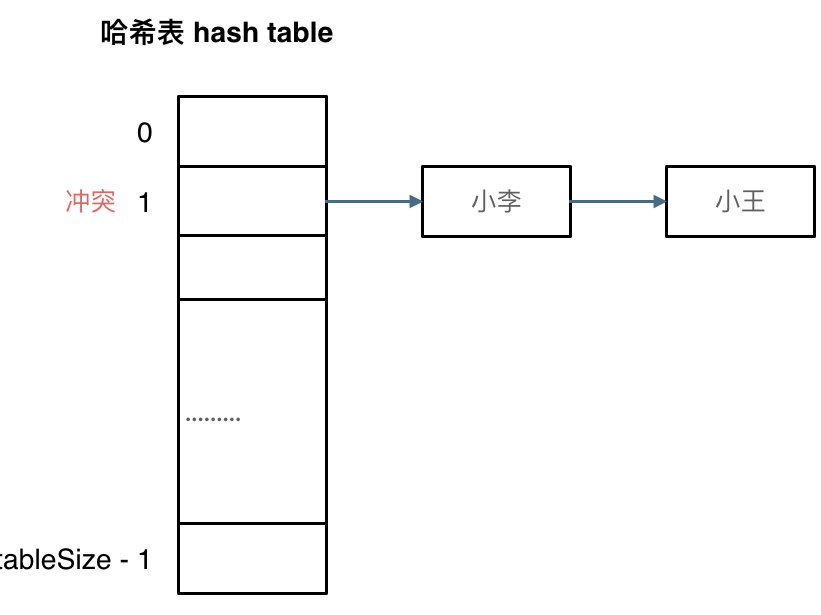
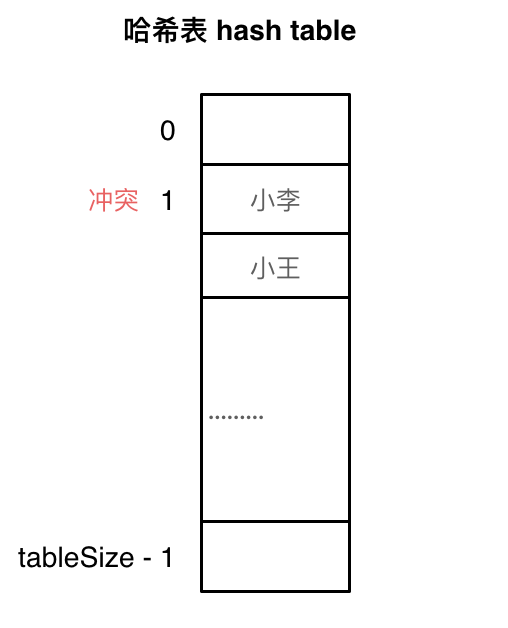
但是可能出现多个键都映射到同一个索引上，这个现象叫哈希碰撞。解决这个问题有两个方案，一个是拉链法，一个是线性探测法。

常见的三种Hash结构

• 数组
• set（集合）
• map（映射）

数组就没啥可说的了。在C++中，set 和 map 分别提供以下三种数据结构，其底层实现以及优劣如下表所示：

集合	实现	是否有序	数值是否可以重复	能否更改数值	查询效率	增删效率
std::set	红黑树	有序	否	否	O(log n)	O(log n)
std::multiset	红黑树	有序	是	否	O(log n)	O(log n)
std::unordered_set	哈希表	无序	否	否	O(1)	O(1)

std::unordered_set底层实现为哈希表，std::set 和std::multiset 的底层实现是红黑树，红黑树是一种平衡二叉搜索树，所以key值是有序的，但key不可以修改，改动key值会导致整棵树的错乱，所以只能删除和增加。

映射	实现	是否有序	数值是否可以重复	能否更改数值	查询效率	增删效率
std::map	红黑树	key有序	key不可重复	key不可修改	O(log n)	O(log n)
std::multimap	红黑树	key有序	key可重复	key不可修改	O(log n)	O(log n)
std::unordered_map	哈希表	key无序	key不可重复	key不可修改	O(1)	O(1)

std::unordered_map 底层实现为哈希表，std::map 和std::multimap 的底层实现是红黑树。同理，std::map 和std::multimap 的key也是有序的（这个问题也经常作为面试题，考察对语言容器底层的理解）。

1、242有效的字母异位词

给定两个字符串 s 和 t ，编写一个函数来判断 t 是否是 s 的字母异位词。
我的思路： 异位词指的就是两个字符串中每个字符出现的次数是相同的。我可以用两个unordered_map统计他们出现的次数，然后比较是否相等。

代码随想录： 这里比较巧妙，他只用一个map去存第一个字符串的元素出现次数。然后去第二个字符串上去遍历，每统计到一个元素就-1，这样如果map所有值都为0就说明两个字符串是异位词。

#include <unordered_map>
class Solution {
public:
    bool isAnagram(string s, string t) {
        if(s.size()!=t.size())return false;
        std::unordered_map<char,int> map1,map2;
        for(int i = 0;i<s.size();i++){
            map1[s[i]]++;
            map2[t[i]]++;
        }
        for(int i = 0;i<s.size();i++){
            if(map1[s[i]]!=map2[s[i]])return false;
        }
        return true;
    }
};

//代码随想录
class Solution {
public:
    bool isAnagram(string s, string t) {
        int record[26] = {0};
        for (int i = 0; i < s.size(); i++) {
            // 并不需要记住字符a的ASCII，只要求出一个相对数值就可以了
            record[s[i] - 'a']++;
        }
        for (int i = 0; i < t.size(); i++) {
            record[t[i] - 'a']--;
        }
        for (int i = 0; i < 26; i++) {
            if (record[i] != 0) {
                // record数组如果有的元素不为零0，说明字符串s和t 一定是谁多了字符或者谁少了字符。
                return false;
            }
        }
        // record数组所有元素都为零0，说明字符串s和t是字母异位词
        return true;
    }
};

2、349两个数组的交集

给定两个数组 nums1 和 nums2 ，返回 它们的交集。输出结果中的每个元素一定是唯一 的。我们可以 不考虑输出结果的顺序 。

tips: 不涉及到排序问题就用Hash容器。这里关键在于只用统计元素是否出现，不用统计他们出现的次数。所以使用unordered_set更好，若是涉及次数的使用unordered_map。

我的思路： 直接用unordered_set统计两个数组出现的元素，然后比较哪些一样。
代码随想录： 用了很多的小tips，例如容器支持迭代器初始化，不用一个一个的放进去。见代码。

#include <unordered_set>
class Solution {
public:
    vector<int> intersection(vector<int>& nums1, vector<int>& nums2) {
        vector<int> inter;
        std::unordered_set<int> set1,set2;
        
        for(int i = 0;i<nums1.size();i++){
            set1.emplace(nums1[i]);
        }
        for(int i = 0;i<nums2.size();i++){
            set2.emplace(nums2[i]);
        }
        for(auto s:set1){
            if(set2.count(s)!=0){
                inter.emplace_back(s);
            }
        }
        return inter;
    }
};

//代码随想录
class Solution {
public:
    vector<int> intersection(vector<int>& nums1, vector<int>& nums2) {
        unordered_set<int> result_set; // 存放结果，之所以用set是为了给结果集去重
        unordered_set<int> nums_set(nums1.begin(), nums1.end());
        for (int num : nums2) {
            // 发现nums2的元素 在nums_set里又出现过
            if (nums_set.find(num) != nums_set.end()) {
                result_set.insert(num);
            }
        }
        return vector<int>(result_set.begin(), result_set.end());
    }
};

3、202快乐数

编写一个算法来判断一个数 n 是不是快乐数。「快乐数」 定义为：

• 对于一个正整数，每一次将该数替换为它每个位置上的数字的平方和。
• 然后重复这个过程直到这个数变为 1，也可能是 无限循环 但始终变不到 1。
• 如果这个过程 结果为 1，那么这个数就是快乐数。
• 如果 n 是 快乐数 就返回 true ；不是，则返回 false 。

我的思路： ：这道题我的第一感觉是快乐数好像没啥特殊性质可以简化迭代，只有一直判断下去到最后才知道是不是快乐数。最后等于1那就是快乐数，最后一直循环了那就不是快乐数。我用一个unordered_set存储出现过的元素，每次生成新元素就进行判断看它是否再集合里，如果在则循环就不是快乐数。
如果对取数值各个位上的单数操作不熟悉的话，做这道题也会比较艰难。 代码随想录的方法如下。

// 我的
#include <unordered_set>
class Solution {
public:
    bool isHappy(int n) {
        std::unordered_set<int> his;

        while(his.find(n)==his.end()){ // 循环条件：没有出现过
            his.emplace(n); // 存储出现过的元素
            auto str_n = std::to_string(n);
            int i = 0;
            n = 0;
            while(i < str_n.size()){
                n+=std::pow((str_n[i]-'0'),2);
                i++;
            }
            if(n==1)return true;
        }
        return false;
    }
};

//代码随想录
// 取数值各个位上的单数之和
int getSum(int n) {
    int sum = 0;
    while (n) { //一直取余
        sum += (n % 10) * (n % 10);
        n /= 10;
    }
    return sum;
}

4、1两数之和

我的思路： ：这道题我想的还是遍历的思想，看快指针之前的元素能不能有和他成对儿的。复杂度是 O(n*n)。
代码随想录 ：使用一个Hashmap去存出现过的元素和它的索引，在迭代的过程中不断判断是否有元素可以和当前元素成对儿。这个map和我的内层for循环是一样的作用，但是却可以以O(1)的复杂度找到目标。

总结tips： 如果你要用循环去找一个数，而这个循环中的大部分元素总是被重复操作，可以考虑使用HashMap。

// 我的
class Solution {
public:
    vector<int> twoSum(vector<int>& nums, int target) {
        for(int i = 0;i<nums.size();i++){
            for(int j =0;j<i;j++){  // O(n)
                if(nums[i]+nums[j]==target){
                    vector<int> re = {i,j};
                    return re;
                }
            }
        }
        return vector<int>();
    }
};

// 代码随想录
class Solution {
public:
    vector<int> twoSum(vector<int>& nums, int target) {
        std::unordered_map<int,int> maps;
        for(int i = 0;i<nums.size();i++){
            auto it = maps.find(target - nums[i]);  // O(1)
            if(it!=maps.end()){
                return vector<int>({i,it->second});
            }
            maps.emplace(nums[i],i);
        }
        return vector<int>();
    }
};