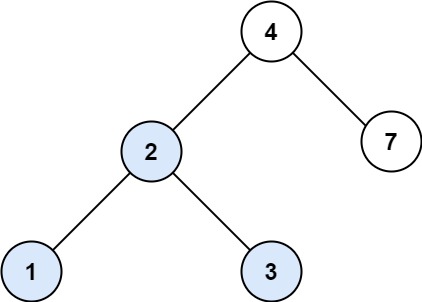
1、654最大二叉树

我的思路：和从前序、中序、后序重构二叉树的框架一样。应该重构二叉树都是一个框架。
代码随想录

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
public:
    TreeNode* traverse(vector<int>& nums, int start, int end){
        if(start > end){
            return nullptr;
        }

        //find max
        int maxval = nums[start];
        int idx = start;
        for(int i = start+1;i<=end;i++){
            if(nums[i] > maxval){
                maxval = nums[i];
                idx = i;
            }
        }

        auto root = new TreeNode(maxval);

        root->left = traverse(nums,start,idx-1);
        root->right = traverse(nums,idx+1,end);
        return root;
    }
    TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
        return traverse(nums,0,nums.size()-1);
    }
};

2、617合并二叉树

我的思路： 这道题还是递归的去构造二叉树就行，由于是两棵树所以参数是两个树节点。
代码随想录： 看了代码随想录之后发现我写的还是太冗余了。对于没有节点的位置我在树上虚拟了一个空节点。其实对于一个子树上没有节点的，直接把另一个树的子树接过来就ok。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
// 我写的
class Solution {
public:
    TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {
        if(root1 == nullptr && root2 == nullptr)return nullptr;
        
        TreeNode* root = nullptr;
        if(root1 != nullptr){
            if(root2!=nullptr){
                root1->val +=root2->val;
                root = root1;
            }
        }else{
            root = root2;
        }
        
        root->left = mergeTrees(root1 == nullptr?nullptr:root1->left,
                                root2 == nullptr?nullptr:root2->left);
        root->right = mergeTrees(root1 == nullptr?nullptr:root1->right,
                                root2 == nullptr?nullptr:root2->right);
        return root;
    }
};
// 看了代码随想录之后写的
class Solution {
public:
    TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {
        if(root1 == nullptr )return root2;
        if(root2 == nullptr )return root1;
        
        root1->val +=root2->val;
        root1->left = mergeTrees(root1->left,root2->left);
        root1->right = mergeTrees(root1->right,root2->right);
        return root1;
    }
};

3、700二叉搜索树中的搜索

给定二叉搜索树（BST）的根节点 root 和一个整数值 val。你需要在 BST 中找到节点值等于 val 的节点。 返回以该节点为根的子树。 如果节点不存在，则返回 null 。
二叉搜索树：也称二叉排序树或二叉查找树。
非空左子树的所有键值小于其根结点的键值。
非空右子树的所有键值大于其根结点的键值。
左、右子树都是二叉搜索树。

我的思路： 利用二叉搜索树的性质就行。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
// 我写的
class Solution {
public:
    TreeNode* searchBST(TreeNode* root, int val) {
        if(root == nullptr || val == root->val)return root;

        if(val < root->val){
            return searchBST(root->left,val);
        }
        if(val > root->val){
            return searchBST(root->right,val);
        }
        return nullptr;
    }
};

4、98验证二叉搜索树

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

遇到二叉搜索树，一定想着中序遍历，这样才能利用上特性。二叉搜索树中不能有重复元素。

我的思路：没做出来。
代码随想录： 代码随想录也是利用这个性质。先中序遍历，再检查遍历结果是否单调。我的和它的区别是我没有保存全部遍历结果，我只保留最后一个元素，节省内存。

二叉搜索树中序遍历特性： 中序遍历下，输出的二叉搜索树节点的数值是有序序列。验证二叉搜索树，就相当于变成了判断一个序列是不是递增的了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
// 了解了 二叉搜索树中序遍历特性 后我写的
class Solution {
public:
    bool traverse(TreeNode* root, TreeNode* &lastnode){
        if(root == nullptr) return true;

        if(traverse(root->left,lastnode) == false)return false; 
        if(lastnode != nullptr && root->val <= lastnode->val){  //中
            return false;
        }
        lastnode = root;
        if(traverse(root->right,lastnode) == false)return false;  
        return true;
    }
    bool isValidBST(TreeNode* root) {
        TreeNode* lastnode = nullptr;
        return traverse(root,lastnode);
    }
};
// 代码随想录
class Solution {
private:
    vector<int> vec;
    void traversal(TreeNode* root) {
        if (root == NULL) return;
        traversal(root->left);
        vec.push_back(root->val); // 将二叉搜索树转换为有序数组
        traversal(root->right);
    }
public:
    bool isValidBST(TreeNode* root) {
        vec.clear(); // 不加这句在leetcode上也可以过，但最好加上
        traversal(root);
        for (int i = 1; i < vec.size(); i++) {
            // 注意要小于等于，搜索树里不能有相同元素
            if (vec[i] <= vec[i - 1]) return false;
        }
        return true;
    }
};