1、513找树左下角的值
给定一个二叉树的 根节点 root,请找出该二叉树的 最底层 最左边 节点的值。假设二叉树中至少有一个节点。

我的思路:这道题for循环的层序遍历最好做。如果递归,就是要找到最大深度的第一个节点。
代码随想录:一样。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
|
class Solution {
public:
int findBottomLeftValue(TreeNode* root) {
if(root==nullptr)return 0;
queue<TreeNode*> pq;
pq.push(root);
TreeNode* target = nullptr;
while(!pq.empty()){
int sz = pq.size();
for(int i = 0;i<sz;i++){
auto node = pq.front();
if(i == 0){
target = node;
}
pq.pop();
if(node->left != nullptr){
pq.push(node->left);
}
if(node->right != nullptr){
pq.push(node->right);
}
}
}
return target->val;
}
};
class Solution {
public:
void traverse(TreeNode* root, int &maxDep,int &val, int curDep){
if(root->left == nullptr && root->right == nullptr){
if(curDep>maxDep){
maxDep = curDep;
val = root->val;
}
return;
}
if(root->left != nullptr){
traverse(root->left,maxDep,val,curDep+1);
}
if(root->right != nullptr){
traverse(root->right,maxDep,val,curDep+1);
}
}
int findBottomLeftValue(TreeNode* root) {
int maxDep = -1, val = 0;
traverse(root,maxDep,val,0);
return val;
}
};
|
2、112路径总和
给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径,这条路径上所有节点值相加等于目标和 targetSum 。如果存在,返回 true ;否则,返回 false 。
我的思路:递归解法。
代码随想录:看了代码随想录后发现可以再继续优化,每次求累加实际上重复了,我们维护一个求和就可以。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
|
class Solution {
public:
bool traverse(TreeNode* root, vector<TreeNode*> &path,int targetSum){
path.emplace_back(root);
if(root->left == nullptr && root->right == nullptr){
int sum = 0;
for(auto &node:path){
sum+=node->val;
}
path.pop_back();
return sum == targetSum?true:false;
}
bool le = false, ri = false;
if(root->left!=nullptr){
le = traverse(root->left,path,targetSum);
if(le == true)return true;
}
if(root->right!=nullptr){
ri = traverse(root->right,path,targetSum);
if(ri == true)return true;
}
path.pop_back();
return false;
}
bool hasPathSum(TreeNode* root, int targetSum) {
if(root == nullptr)return false;
vector<TreeNode*> path;
return traverse(root,path,targetSum);
}
};
class Solution {
public:
bool traverse(TreeNode* root, int sum,int targetSum){
if(root->left == nullptr && root->right == nullptr){
return sum == targetSum?true:false;
}
bool le = false, ri = false;
if(root->left!=nullptr){
le = traverse(root->left,sum+root->left->val,targetSum);
if(le == true)return true;
}
if(root->right!=nullptr){
ri = traverse(root->right,sum+root->right->val,targetSum);
if(ri == true)return true;
}
return false;
}
bool hasPathSum(TreeNode* root, int targetSum) {
if(root == nullptr)return false;
return traverse(root,root->val,targetSum);
}
};
|
3、113路径综合II
给你二叉树的根节点 root 和一个整数目标和 targetSum ,找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。叶子节点 是指没有子节点的节点。
我的思路: 关键在于求路径那就需要记录路径,顺序路径意味着前序遍历。
代码随想录: 一样。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
| class Solution {
public:
void traverse(TreeNode* root,vector<vector<int>> &paths, vector<int> &path, int sum,int targetSum){
path.emplace_back(root->val);
if(root->left == nullptr && root->right == nullptr){
if(sum == targetSum){
paths.emplace_back(path);
}
path.pop_back();
return;
}
if(root->left!=nullptr){
traverse(root->left,paths,path,sum+root->left->val,targetSum);
}
if(root->right!=nullptr){
traverse(root->right,paths,path,sum+root->right->val,targetSum);
}
path.pop_back();
return;
}
vector<vector<int>> pathSum(TreeNode* root, int targetSum) {
if(root == nullptr)return vector<vector<int>>();
vector<vector<int>> paths;
vector<int> path;
traverse(root,paths,path,root->val,targetSum);
return paths;
}
};
|
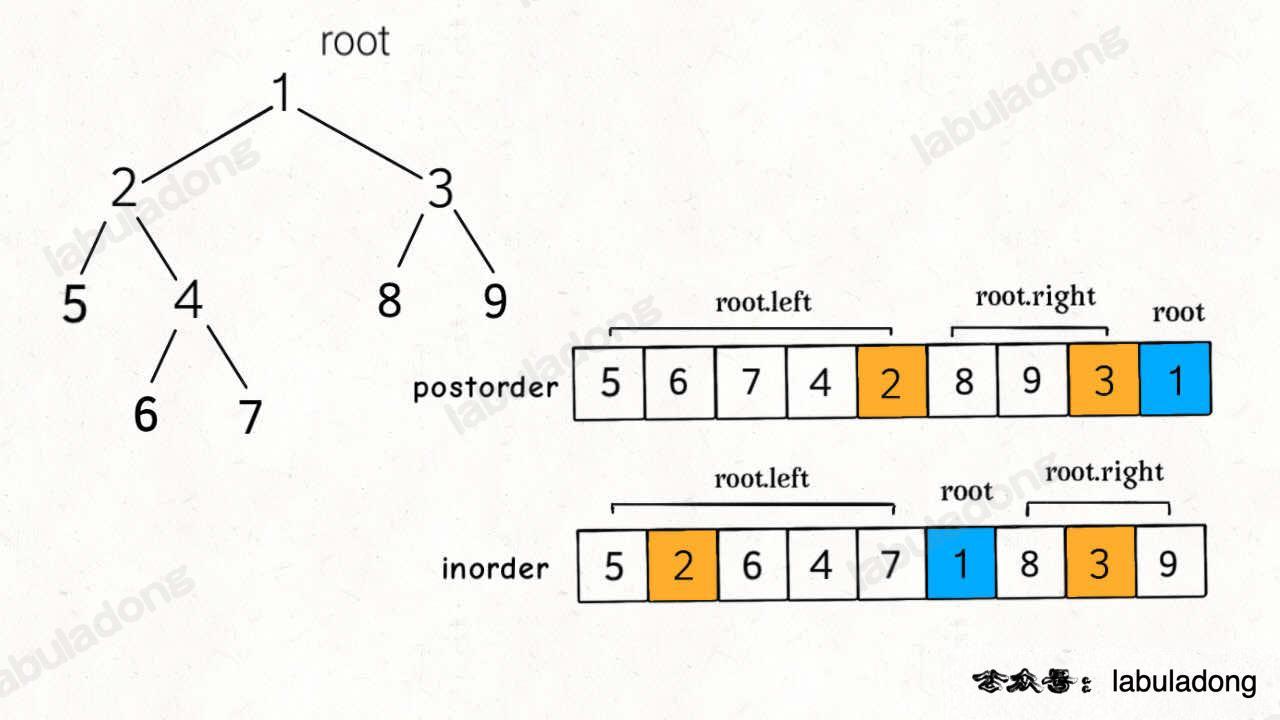
4、106从中序与后序遍历序列构造二叉树
给定两个整数数组 inorder 和 postorder ,其中 inorder 是二叉树的中序遍历, postorder 是同一棵树的后序遍历,请你构造并返回这颗 二叉树 。

我的思路: 没做出来。核心还是要熟二叉树的前中后遍历结果。
labuladong
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
|
class Solution {
public:
TreeNode* traverse(vector<int>& inorder, vector<int>& postorder,
int instart, int inend, int poststart, int postend){
if(instart > inend){
return nullptr;
}
auto root = new TreeNode(postorder[postend]);
int rootidx = 0;
for(rootidx = instart; rootidx<= inend; rootidx++){
if(inorder[rootidx] == root->val){
break;
}
}
int lftsize = rootidx - instart;
int rgtsize = inend - rootidx;
root->left = traverse(inorder,postorder,instart,rootidx-1,poststart,poststart+lftsize-1);
root->right = traverse(inorder,postorder,rootidx+1,inend,poststart+lftsize,postend-1);
return root;
}
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
return traverse(inorder,postorder,0,inorder.size()-1,0,postorder.size()-1);
}
};
|
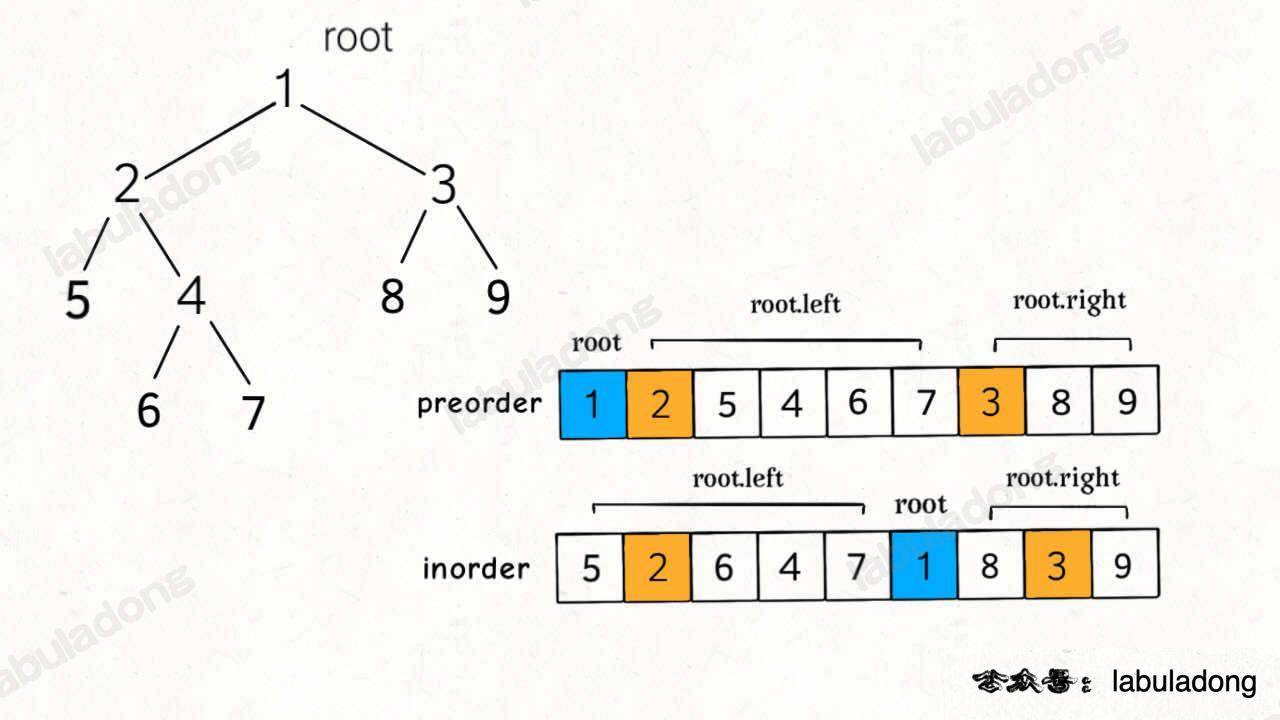
5、105从前序与中序遍历序列构造二叉树

我的思路: 和106一样。核心还是要熟二叉树的前中后遍历结果。
labuladong
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
|
class Solution {
public:
TreeNode* traverse(vector<int>& inorder, vector<int>& preorder,
int instart, int inend, int prestart, int preend){
if(instart > inend){
return nullptr;
}
auto root = new TreeNode(preorder[prestart]);
int rootidx = 0;
for(rootidx = instart; rootidx<= inend; rootidx++){
if(inorder[rootidx] == root->val){
break;
}
}
int lftsize = rootidx - instart;
root->left = traverse(inorder,preorder,instart,rootidx-1,prestart+1,prestart+lftsize);
root->right = traverse(inorder,preorder,rootidx+1,inend,prestart+lftsize+1,preend);
return root;
}
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
return traverse(inorder,preorder,0,inorder.size()-1,0,preorder.size()-1);
}
};
|
代码随想录算法训练第十六天|513找树左下角的值|112路径总和|113路径综合II|106从中序与后序遍历序列构造二叉树|105从前序与中序遍历序列构造二叉树