1、曲率的定义

曲率（Curvature）是描述曲线弯曲程度的量度。在二维空间中，对于一条曲线，曲率在某一点上可以通过以下公式计算：
$$
\kappa = \frac{d\theta}{ds}
$$
其中：

dθ是曲线的切线方向（即车辆朝向）相对于路径切线的变化量。
ds是路径上的微小弧长增量。

2、曲率的大小和方向

大小： 曲率的大小表示曲线弯曲的程度，曲线弯曲的越大，其曲率越大。
方向： 曲率的正负决定了路径的弯曲方向。遵循右手定则，正曲率表示曲线逆时针弯曲，负曲率表示顺时针弯曲。

3、曲率的应用

3.1 曲率的计算

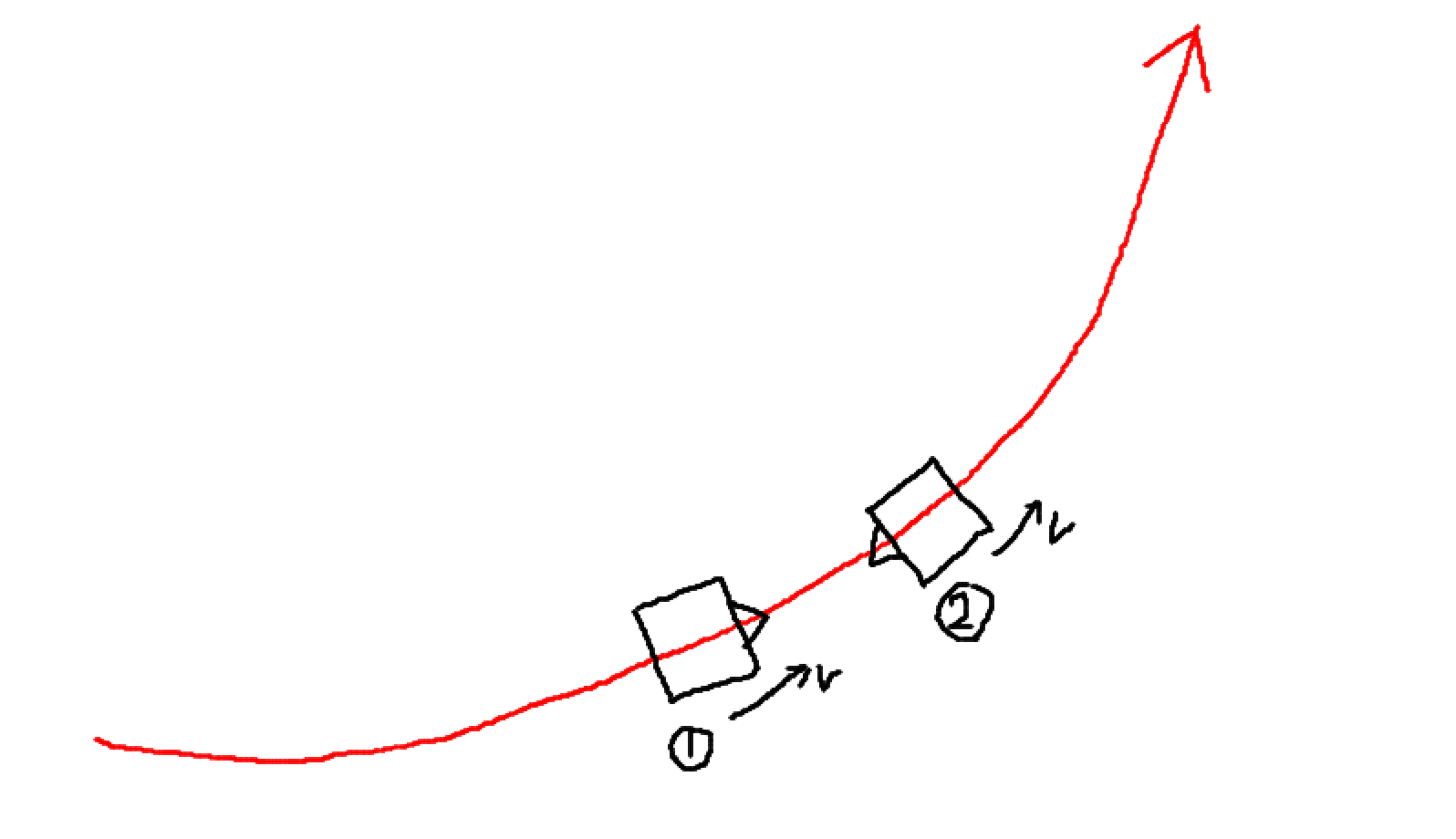
在自动驾驶中，车辆的转弯半径受到前轮转角的限制，从而影响轨迹的曲率。现在有一条正曲率的轨迹，我们分情况讨论一下曲率：

case 1. 一号车的方向是顺着轨迹的，想要跟踪这条轨迹只需要保持速度为正$v>0$并向左打方向盘，$\delta>0, tan(\delta)>0$。轨迹曲率如下：
$$
\kappa = \frac{1}{R} = \frac{tan\delta}{L}
$$
case 2. 二号车的方向是相反轨迹的，想要跟踪这条轨迹则需要倒车，$v<0$ 并向右打方向盘，$\delta<0,tan(\delta)<0$。轨迹曲率如下：
$$
\kappa = -\frac{tan\delta}{L}
$$

总结：
综上，轨迹的曲率与车辆的运动关系可以表示为如下形式，$sign$ 是符号函数。
$$
\kappa = sign(v)\cdot \frac{tan\delta}{L}
$$

上述公式同样适用于其他非完整模型车辆